
문제 지문 #2
다음과 같이 n x n 크기의 격자에 1부터 n x n까지의 수가 하나씩 있습니다.

이때 수가 다음과 같은 순서로 배치되어있다면 이것을 n-소용돌이 수라고 부릅니다.
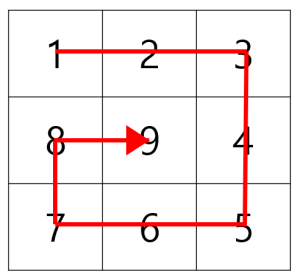
소용돌이 수에서 1행 1열부터 n 행 n 열까지 대각선 상에 존재하는 수들의 합을 구해야 합니다.
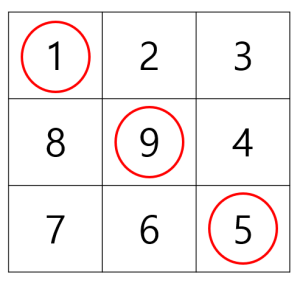
위의 예에서 대각선 상에 존재하는 수의 합은 15입니다.
격자의 크기 n이 주어질 때 n-소용돌이 수의 대각선 상에 존재하는 수들의 합을 return 하도록 solution 메서드를 완성해주세요.
매개변수 설명
격자의 크기 n이 solution 메서드의 매개변수로 주어집니다.
- n은 1 이상 100 이하의 자연수입니다.
return 값 설명
n-소용돌이 수의 대각선 상에 존재하는 수들의 합을 return 해주세요.
예시
| n | return |
|---|---|
| 3 | 15 |
| 2 | 4 |
예시 설명
예시 #1
문제의 예와 같습니다.
예시 #2
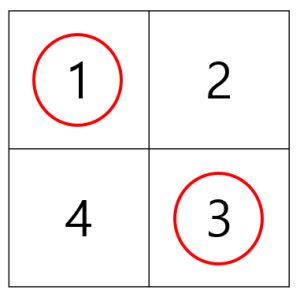
1과 3을 더하여 4가 됩니다.
혼자 풀이
1시간 넘게 걸렸습니다...
소용돌이수는 순차적으로 열 방향 증가, 행 방향 증가, 열 방향 감소, 행 방향 감소 4가지 패턴을 반복하는 것으로 보입니다. 그래서 n×n배열의 원소를 0으로 초기화한 후, 입력 위치의 값이 0일 때는 p_num을 넣고,
0이 아닌 값을 만나면 다음 패턴으로 넘어가면서 p_num이 입력된 n의 제곱이 될 때까지 루프 문을 반복합니다.
반복이 끝나면 대각선의 값을 합해서 리턴합니다.
비슷한 for문과 if문이 여러번 등장하는 것이 보기 안 좋아서 공통화하고 싶은데, 방법을 못 찾았습니다.
/**************************************************
1차 2번 소용돌이 수의 대각선 합계 구하기
*************************************************/
class MySolution {
public int solution(int n) {
// Write code here.
int answer = 0;
//소용돌이 수는 열 증가 행 증가 열감소 행 감소 순으로 반복해서 진행된다.
//4X4 배열에 값을 넣으면서 값이 0이 아니면 다음으로 진행하면 됨
//배열 초기화
int twistArray[][]=new int[n][n];
for(int i=0;i<n;i++){
for(int j=0;j<n;j++){
twistArray[i][j]=0;
}
}
int p_num=1; //배열에 입력하는 소용돌이 수
int i=0;
int j=0;
while(true){
while(j<n) {
//p_num을 입력할 곳이 0으로 초기화 되어있는 경우에만 입력
if (twistArray[i][j] == 0) {
twistArray[i][j] = p_num;
p_num++;
} else { //break 전 루프에서 j를 증가시켰으니 다시 감소시키고, 다음 입력위치로 조정
j--;
i++;
break;
}
j++;
if(j==n) {//j가 n에 도달하면 break;
j--;
i++;
break;
}
}
while(i<n) {
//p_num을 입력할 곳이 0으로 초기화 되어있는 경우에만 입력
if (twistArray[i][j] == 0) {
twistArray[i][j] = p_num;
p_num++;
} else { //break 전 루프에서 i를 증가시켰으니 다시 감소시키고, 다음 입력위치로 조정
j--;
i--;
break;
}
i++;
if(i==n) {//i가 n에 도달하면 break;
i--;
j--;
break;
}
}
while(j>=0) {
//p_num을 입력할 곳이 0으로 초기화 되어있는 경우에만 입력
if (twistArray[i][j] == 0) {
twistArray[i][j] = p_num;
p_num++;
} else {//break 전 루프에서 j를 감소시켰으니 다시 증가시키고, 다음 입력위치로 조정
j++;
i--;
break;
}
j--;
if(j<0) {//i가 0에 도달하면 break;
j++;
i--;
break;
}
}
while(i>=0) {
//p_num을 입력할 곳이 0으로 초기화 되어있는 경우에만 입력
if (twistArray[i][j] == 0) {
twistArray[i][j] = p_num;
p_num++;
} else {//break 전 루프에서 i를 감소시켰으니 다시 증가시키고, 다음 입력위치로 조정
i++;
j++;
break;
}
i--;
if(i==0) {//i가 0에 도달하면 break; j는 0보다 작아질 수 있지만, i는 0보다 작을 일이 없음
i++;
j++;
break;
}
}
if(p_num>n*n) break;
}
//대각선 합계
for(int k=0;k<n;k++){
answer+=twistArray[k][k];
}
return answer;
}
// The following is main method to output testcase.
public static void main(String[] args) {
MySolution sol = new MySolution();
int n1 = 3;
int ret1 = sol.solution(n1);
// Press Run button to receive output.
System.out.println("MySolution: return value of the method is " + ret1 + " .");
int n2 = 2;
int ret2 = sol.solution(n2);
// Press Run button to receive output.
System.out.println("MySolution: return value of the method is " + ret2 + " .");
}
}정답 파일 보니, 기본적으로 4가지 패턴이 반복되는 건 맞습니다만, 4가지 패턴을 dx, dy 배열의 조합으로 표현했습니다.
그리고 inRange 함수를 정의해서 범위 내에 속하는지를 체크했네요. 이렇게 하니까 비슷한 코드들이 하나로 묶였다는 것을 알 수 있었습니다.
//정답 파일
lass Solution{
int[][] pane;
int dx[] = {0, 1, 0, -1};
int dy[] = {1, 0, -1, 0};
boolean inRange(int i, int j, int n){
return 0 <= i && i < n && 0 <= j && j < n;
}
public int solution(int n){
pane = new int[n][n];
int ci = 0;
int cj = 0;
int num = 1;
while(inRange(ci, cj, n) && pane[ci][cj] == 0){
for(int k = 0; k < 4; k++){
if(!inRange(ci, cj, n) || pane[ci][cj] != 0) break;
while(true){
pane[ci][cj] = num++;
int ni = ci + dy[k];
int nj = cj + dx[k];
if(!inRange(ni, nj, n) || pane[ni][nj] != 0){
ci += dy[(k + 1) % 4];
cj += dx[(k + 1) % 4];
break;
}
ci = ni;
cj = nj;
}
}
}
int ans = 0;
for(int i = 0; i < n; i++) ans += pane[i][i];
return ans;
}
}첨부 파일
프로젝트 파일 전체를 첨부합니다.
Solution 이 문제, CorrectSolution 이 정답, MySolution이 제가 푼 것입니다.
"Project from existing sources..." 메뉴에서 불러다 쓰시면 됩니다.
출처: https://www.ybmit.com/cos_pro/cos_pro_r_test.jsp
'Programming > Cos Pro 1급' 카테고리의 다른 글
| Cos Pro 1급 - 샘플 문제 풀이 1차 4번 (배열 가지고 놀기) (0) | 2022.10.06 |
|---|---|
| Cos Pro 1급 - 샘플 문제 풀이 1차 3번 (Ascii 코드 활용) (0) | 2022.10.05 |
| Cos Pro 1급 - 샘플 문제 로드하는 방법 (0) | 2022.10.03 |
| Cos Pro 1급 - 샘플 문제 풀이 1차 1번 (자연수의 각 자리별 접근) (0) | 2022.09.29 |
| COS Pro 1급 시험 준비 (2) | 2022.09.29 |




댓글